Homogeneous Reactor Flamelet Generation
Overview
The process of generating a suite of Homogeneous-Reactor flamelets that can then be processed into a flamelet table is quite different from that used for 1D diffusion flamelets. With diffusion flamelets (generated using either FlameMaster or Cantera), the typical process involves an automated marching process around the so-called S-curve, in which each point on the S-curve is a distinct flamelet solution at a given strain rate located either on the burning branch, the unstable branch, or the pure-mixing branch. In regards to the Z dimension of the table, each diffusion flamelet spans the entire dimension range (0 < Z < 1), where Z = 0 is pure oxidizer, Z = 1 is pure fuel, and intermediate values contain combusted states and the main flame. When one attempts to aggregate these flamelets into a flamelet table, often a pruning process is required to prevent overlap of neighboring diffusion flamelets in regards to the progress variable dimension (C), which can produce unphysical jumps in the tabulated variables with the final flamelet table. In this regard, it is important to note that flamelet pruning is an inter-flamelet process which involves comparisons between multiple flamelets.
In contrast to diffusion flamelets, individual Homogeneous-Reactor flamelets do not span the Z dimension of the table. In fact, each flamelet corresponds to a single Z value. Consider the diagram shown below.
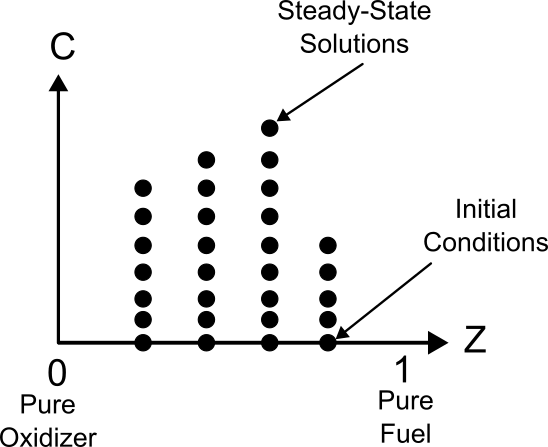
Simple diagram showing how the homogeneous-reactor flamelets fill the Z-C space.
At any particular value of Z, one specifies a Homogeneous-Reactor initial condition (the C = 0 state) for pressure, specific enthalpy, and species mass fractions by combining the fuel and oxidizer according to the relations shown below.
This initial state is then integrated in time to the final fully-combusted steady-state condition, which is represented in the figure by a vertical line at the given Z value. Having generated all of the individual Homogeneous-Reactor flamelets (one for each Z value), these values can then be aggregated into a flamelet table. Depending on the definition of C, one may need to perform pruning of the flamelets to achieve monotonic C evolution within each homogeneous reactor, but unlike diffusion flamelets, the pruning of any one homogeneous-reactor flamelet is completely independent of the solution in all the other flamelets.
The homogeneous reactor has several utilities in addition to the flamelet generator. These utilities are:
Binary |
Description |
|---|---|
|
Allows a user to examine the equation of state (EOS) that is used in the homogeneous reactor. |
|
The primary tool in the homogeneous reactor for generating flamelets. |
|
A 0D reactor that supports constant pressure or constant volume time integration. |
Handling of Two-Phase Combustion
A gas-phase reaction mechanism augmented with a liquid-phase reaction, phase-state information provided by the Complete Peng-Robinson Equation of State (CPREOS) is required by the reaction library to determine which elements of the complete reaction set are active. The primary principles at play in the method are:
When the mixture is in the liquid phase, only the global liquid reaction is active.
When the mixture is in the vapor phase, only the gas-phase reaction mechanism is active.
When the mixture is two-phase, both the global liquid reaction and the gas-phase mechanism are active.
Consider the p-v phase diagram shown in the image below.
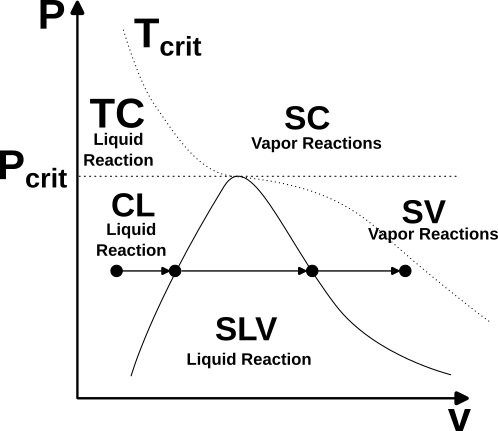
Phase diagram showing the regions of the space and the corresponding vapor quality values.
The CPREOS stores not only thermodynamic state variables (such as density, pressure, temperature, etc.), but also the vapor quality of the mixture, designated by the symbol q. The various regions of the space are designated as follows:
CL: Compressed liquid region (P < P_Crit, T < T_Sat)
SLV: Saturated liquid-vapor region (P < P_Crit, T = T_Sat)
SV: Superheated vapor region (P < P_Crit, T > T_Sat)
TC: Transcritical region (P < P_Crit, T > T_Crit)
SC: Supercritical region (P > P_Crit, T > T_Crit)
where P_Crit is the critical pressure, T_Crit is the critical temperature, and T_Sat is the saturation temperature of the current mixture (defined by the molar or mass composition). In the figure, for each of these regions, the corresponding vapor quality value is shown. We note that in the TC region, while the mixture is technically not in a true liquid state, as in the CL region, we have defined a vapor quality of q = 0, so that liquid-liquid combustion simulations can be initiated with the high-density, liquid-like reactant mixtures located there. From these values, we see the following reaction characteristics:
CL, TC: Only global liquid reaction is active
SLV: Both global liquid reaction and gas-phase reaction mechanism active
SV, SC: Only gas-phase reaction mechanism active
These conditions are enforced within the reaction kinetics coding of the Homogeneous Reactor in a relatively simple manner by modifying the concentration of the reactants using the molar vapor quality. Assume, for example, that we have the following liquid reaction:
A + B -> C + D + E + F
The production rate of species C is typically written as follows:
where \(K_f\) is the forward reaction rate in standard Arrhenius rate form, and \(|*|\) represents the molar concentration of any species. However, when dealing with combined mechanisms (containing the liquid reaction and the gas-phase reaction mechanism), the total concentration of species A and B may be distributed between liquid and vapor phases. Because the liquid reaction must only consume the liquid parts of A and B available in the mixture, the production rate of species C in this example is modified to the following:
From this new form, it is clear that when \(q = 1\) (the mixture is 100% vapor), the liquid reaction ceases to produce species C, D, E, and F. A similar strategy is used for the gas-phase mechanism reactions. Consider the following generic forward/reverse elementary reaction that is typical in standard gas-phase mechanisms (this is only one of the reactions in the complete gas-phase mechanism):
G + H <-> I + J
The contribution to the net production rate of species I from this reaction alone is typically written as follows:
where \(K_r\) is the reverse reaction rate in standard Arrhenius form. Since the species I is by definition only to be produced via the reaction of vapor-phase G and H and depleted by the reaction of vapor-phase I and J, the net production rate must be modified to the following:
In a manner similar to the liquid reaction above, when \(q = 0\), the reaction ceases to produce species I (as well as species G, H, and J).
Using Homogeneous-Reactor Flamelets with the Flamelet Table Tool
To use the Homogeneous-Reactor flamelets with the Flamelet Table Tool, the FLAMELETTYPE option in the control file must be set to
homogeneous_reactor. The FUEL option must also be set to the name of the fuel species. An example of the control file options
required for generating flamelet tables using Homogeneous-Reactor flamelets is shown below.
FLAMELETTYPE homogeneous_reactor
FUEL H2
The FUEL is simply the name of the species that is the fuel in the flames.
Flamelet Generation
The flamelet-generator is available to automate the process of generating a suite of 0D flamelets over the Z-space of a
flamelet table. This tool employs essentially the same methods as the reactor tool, but unlike the reactor tool, given a
complete specification of the fuel and the oxidizer, the tool will perform all homogeneous-reactor simulations required to span
the entire Z space at a user-specified resolution. A sample execution command for flamelet-generator is shown below.
flamelet-generator -crit critical-properties -mech H2_ideal -n 201 -P 5.4e+06 -Tf 800 -yf H2 0.4018 -yf H2O 0.5982 -To 711 -yo O2 0.9449 -yo H2O 0.0551 -time 20.0 -of 1 -atol 1.0e-15 -rtol 1.0e-09
The flamelet-generator generates constant pressure solutions. The example above specifies a case where the fuel is a mixture of H2 and
H2O, and the oxidizer is a mixture of O2 and H2O. The mass fractions of the fuel and oxidizer are specified using the -yf and -yo
options, respectively. The temperature of the fuel and oxidizer is specified using the -Tf and -To options, respectively. The
pressure is specified using the -P option. The number of Z points is specified using the -n option. The time to integrate the
homogeneous reactor is specified using the -time option. The output frequency is specified using the -of option. The absolute
tolerance is specified using the -atol option, and the relative tolerance is specified using the -rtol option.
This will generate a set of solutions with the naming convention flamelet_#.dat, where # is the integer index of the Z value, for example
if -n 10 is provided, then flamelet_0.dat, flamelet_1.dat, ..., flamelet_9.dat will be generated.
Creating a YAML Mechanism File
The Homogeneous-Reactor flamelet-generator requires a YAML mechanism file to run. This mechanism file is derived from the Cantera
YAML mechanism file format.
Specification Reactions Involving Liquid Components
Some additional steps are required by the user in specifying species in mechanisms intended to be used for two-phase combustion simulations. The goal of these steps is to aid the reactor library in enforcing the three principles described earlier. A modified syntax .yaml mechanism file is introduced to aid the reactor library.
The gas-phase mechanism RChem3, which is augmented with the liquid reaction shown below will be used to demonstrate this syntax. The liquid reaction is:
equation: CH3NHNH2 + 8.5 NO2 => CO2 + 3 H2O + 2.25 N2 + 6 NO + 3 O2
For a pure gas-phase combustion problem using the RChem3 mechanism, the species subsection of the phases section of the .yaml file looks as follows:
species: [H, H2, O, OH, H2O, HO2, CH2, CH3, CH4, CO, HCO, CH2O, CH3O,
CO2, N, NH, NH2, NH3, N2, NNH, N2H2, NO, HNO, N2O, NO2, HONO, HNO3,
N2O4, CN, HCN, HNC, NCO, CH3NHNH2, CH2NHNH2, CH3NNH2, CH3NHNH, CH3NN,
CH2NNH2, HNCO, CH3NNH, CH3ONO2, AR, O2, H2O2]
In order to assist the reactor library in parsing reactions for the augmented mechanism file that contains the additional liquid reaction, this section must be changed to the following:
species: [H, H2, O, OH, H2O_*, HO2, CH2, CH3, CH4, CO, HCO, CH2O, CH3O,
CO2_*, N, NH, NH2, NH3, N2_*, NNH, N2H2, NO_*, HNO, N2O, NO2_*, HONO, HNO3,
N2O4, CN, HCN, HNC, NCO, CH3NHNH2_*, CH2NHNH2, CH3NNH2, CH3NHNH, CH3NN,
CH2NNH2, HNCO, CH3NNH, CH3ONO2, AR, O2_*, H2O2]
Here, an _ * has been appended to selected species. These selected species are designated as the “two-phase” species
and require augmentation to their names when used later in the mechanism to inform the reaction library which phase of
the species is to be used in a particular reaction. As a general rule, the “two-phase” species list must include all of
the species in the liquid reaction. In this example, all of the species in Equation _ are tagged with the _ * specification.
For the liquid reaction, one must tag the reactants with the _L tag as shown below:
equation: CH3NHNH2_L + 8.5 NO2_L => CO2 + 3 H2O + 2.25 N2 + 6 NO + 3 O2
This tag explicitly tells the reaction library to pre-multiply the concentrations of these reactants by \((1-q)\) when
computing the rates of production of the product species in the liquid equation. In a similar manner, the two-phase species
involved in any of the elementary reactions of the gas-phase part of the mechanism must be tagged with the _V specification.
This tag explicitly tells the reaction library to pre-multiply the concentrations of these reactants by \(q\) when computing
rates of production.
Below are examples of equations from the gas-phase RChem3 mechanism that have been tagged appropriately.
equation: OH + CO <=> H + CO2_V
equation: OH + HCO <=> H2O_V + CO
equation: NNH <=> N2_V + H
equation: N + OH <=> NO_V + H
equation: NH2 + NO_V <=> N2_V + H2O_V
Note: In all of these gas-phase reactions, the concentrations of the untagged species are not, by definition, multiplied by the factor q since the entire concentration must be used. This is because these species are only produced and consumed in the gas-phase reaction set.
Marking Equation of State for Ideal-Gas Species
When the YAML mechanism file is parsed by the reactor library, it constructs the Peng-Robinson equation of state (EOS) for
the mixture. Species that are not explicitly marked as ideal gases in the mechanism file are assumed to be real gases and
thus their critical properties are searched for in the critical-properties.yaml database file. For species that are ideal,
an equation-of-state section must be added to the species entry in the mechanism file. An example of this is shown below for
marking a species as an ideal gas.
phases:
- name: H
composition: {H: 1}
thermo:
model: NASA7
temperature-ranges: [200.0, 1000.0, 3500.0]
data:
- [2.5, 7.05332819e-13, -1.99591964e-15, 2.30081632e-18, -9.27732332e-22,
2.54736599e+04, -0.446682853]
- [2.50000001, -2.30842973e-11, 1.61561948e-14, -4.73515235e-18, 4.98197357e-22,
2.54736599e+04, -0.446682914]
transport:
model: gas
geometry: atom
diameter: 2.05
well-depth: 145.0
equation-of-state:
model: Peng-Robinson
a: 0
b: 0
acentric-factor: 0
Critical Properties File
Any species that is tagged using the _ * marker in the input YAML mechanism file must have its critical properties defined in a file named critical_properties.yaml. This file must be located in the same directory as the input YAML mechanism file. The critical properties file must be in the format shown below. Is has the same format at the standard Cantera critical properties file.
description: |-
These critical properties are used to calculate the a and b parameters for real gas
equations of state, such as Redlich-Kwong and Peng-Robinson.
The a and b parameters can be provided explicitly by the user in the input file. In
the case that they are not provided for a species, and the critical state for the
species is not given in the 'critical-parameters' field of the species entry, Cantera
will search this database for critical properties. If critical properties are not
found and coefficients are not provided, then an error is thrown.
Critical pressures are given in Pa. Critical volumes are given in m^3/kmol.
These critical properties have been compiled from various sources by
C. Karakaya (https://orcid.org/0000-0001-5102-5476)
Notes
1) CH3NHNH2 properties from Physical and Thermodynamic Properties of Hypergolic Propellants - A Review and Update (Arnold 1999)
input-files: critProperties.xml
cantera-version: 2.6.0a3
date: Sat, 20 Nov 2021 22:47:06 -0500
species:
- name: CH3NHNH2
descriptive-name: mmh
molecular-weight: 46.07
critical-parameters:
critical-temperature: 567
critical-pressure: 8.3491e+6
critical-molar-volume: 0.2712
critical-compressibility: 0.474
acentric-factor: 0.425
- name: N2O4
descriptive-name: nitrogen-tetroxide
molecular-weight: 92.02
critical-parameters:
critical-temperature: 431.4
critical-pressure: 1.023e+07
critical-molar-volume: 0.1678
critical-compressibility: 0.473
acentric-factor: 0.834
- name: NO2
descriptive-name: nitrogen-dioxide
molecular-weight: 46.01
critical-parameters:
critical-temperature: 431.4
critical-pressure: 1.013e+07
critical-molar-volume: 0.1697
critical-compressibility: 0.4793
acentric-factor: 0.851
- name: CO2
descriptive-name: carbon-dioxide
molecular-weight: 44.01
critical-parameters:
critical-temperature: 304.2
critical-pressure: 7.39e+06
critical-molar-volume: 0.0948
critical-compressibility: 0.275
acentric-factor: 0.228
- name: H2O
descriptive-name: water
molecular-weight: 18.0153
critical-parameters:
critical-temperature: 647.13
critical-pressure: 2.194e+07
critical-molar-volume: 0.056
critical-compressibility: 0.228
acentric-factor: 0.343
- name: N2
descriptive-name: nitrogen
molecular-weight: 28.02
critical-parameters:
critical-temperature: 126.2
critical-pressure: 3.39e+06
critical-molar-volume: 0.089
critical-compressibility: 0.288
acentric-factor: 0.037
- name: NO
descriptive-name: nitric-oxide
molecular-weight: 30.01
critical-parameters:
critical-temperature: 180.15
critical-pressure: 6.52e+06
critical-molar-volume: 0.058
critical-compressibility: 0.252
acentric-factor: 0.585
- name: O2
descriptive-name: oxygen
molecular-weight: 31.999
critical-parameters:
critical-temperature: 154.58
critical-pressure: 5.02e+06
critical-molar-volume: 0.074
critical-compressibility: 0.287
acentric-factor: 0.020
General Guidance
The Homogeneous-Reactor parses the input YAML file assuming that the order of the species at the top of the mechanism file is the same order that the species entries lower in the file will appear.