Flamelet Introduction
This guide aims to serve as a pragmatic engineering guide to using flamelet modeling for solving combusting flow problems. A flamelet solution is the building-block of a flamelet table. Flamelet modeling is a computationally efficient method for simulating time-accurate, 3D combustion problems involving complex chemistry [ODBB2016] . The flamelet model requires a table containing several hundred flamelet solutions to be generated prior to a CFD simulation. A flamelet table is comprised of many individual solutions to the flamelet equations at CFD simulation-specific conditions that are parameterized by a flamelet progress variable and mixture fraction. Flamelet solutions can be computed using chemical kinetics software such as Cantera or FlameMaster.
For nonpremixed flamelet generation, counter-flow diffusion flame simulations are performed on a 1-D grid with user-defined fuel and oxidizer conditions entering the domain on opposite sides.
FlameMaster solves the counter-flow diffusion flame problem for a range of scalar dissipation rates (related to strain rate). These solutions cover the space of conditions that are used to create a flamelet table.
Cantera solves the counter-flow diffusion flame problem for a range of strain rates directly. These solutions also cover the space of conditions that are used to create a flamelet table.
The collection of individual flamelets can be processed to generate a flamelet table.
FlameMaster is a code developed to solve complex chemical kinetics problems. It is used to compute the solution to 1D counter-flow diffusion flames,
which are used to generate a flamelet table. Complete instructions for installing FlameMaster are in the FlameMaster source code at:
FlameMaster/Documentation/FlameMaster_UserGuide.pdf. The version that is required is anything greater than 3.3.10 (which includes real fluids).
Turbulence Closures
The thickened flame closure method is used for compressible flamelet tables. It is more of a non-closure in the sense that the closure is done in the simulation code and not during the flamelet table generation phase. The thickened flame flamelet tables (for diffusion or premixed flamelets) are new table output formats that are used primarily for the PEC framework. Most users will be using the thickened flame turbulence closure tables. Support for the beta-PDF turbulence closure is also available for diffusion flamelets. The beta-PDF turbulence closure is a closure that is done during the flamelet table generation phase, with the turbulence effects being included in the flamelet table in the form of an additional table dimension.
Compressible Flamelet Table
The compressible flamelet table formulation is based on [1]. It involves the tabulation of ideal and real-gas coefficients directly into the flamelet table. A Peng-Robinson EOS implementation was added to the flamelet table tool to provide the cubic equation of state parameters to the flamelet table, and the open-source tool Cantera was utilized to tabulate the ideal gas quantities of interest as well as transport properties for the various species involved with a reaction mechanism. The CoolProp open-source python module was also utilized to obtain the real fluid transport properties. This capability is activated using the FPVC input file keyword to the Flamelet Table Tool.
Non-Premixed (Diffusion) Flamelet Capability
Non-premixed flamelet tables are generated by solving counterflow diffusion flames for various values of the flow strain rate. This is currently done using the FlameMaster software. These flamelets are solved in the mixture fraction space(Z) and are represented by one dimensional data. These flamelets represent the solution to a one-dimensional problem where two boundaries in a counter-flow configuration emit a fuel and oxidizer stream and a flame forms somewhere between the two boundaries depending on the rate of strain of the flow between the two surfaces (which in the physical space is brought about by the velocity condition on each boundary).
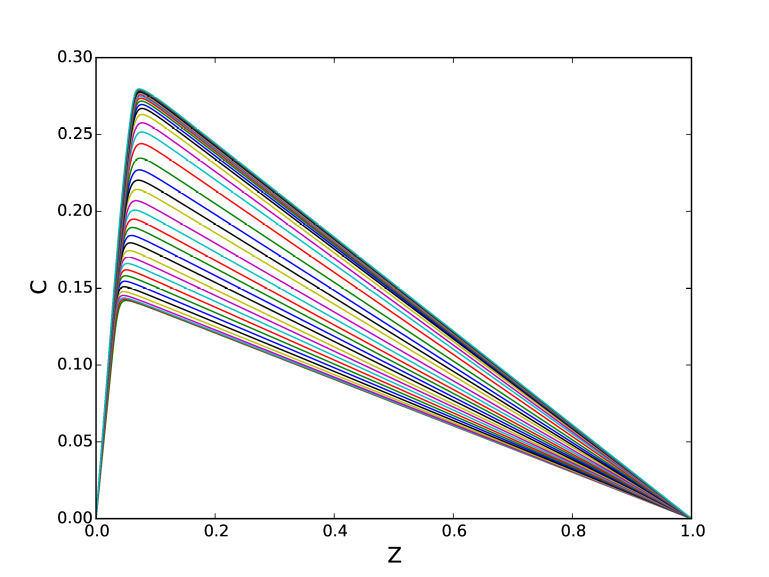
Diffusion flamelets that compose the manifold space for generating a non-premixed flamelet table.
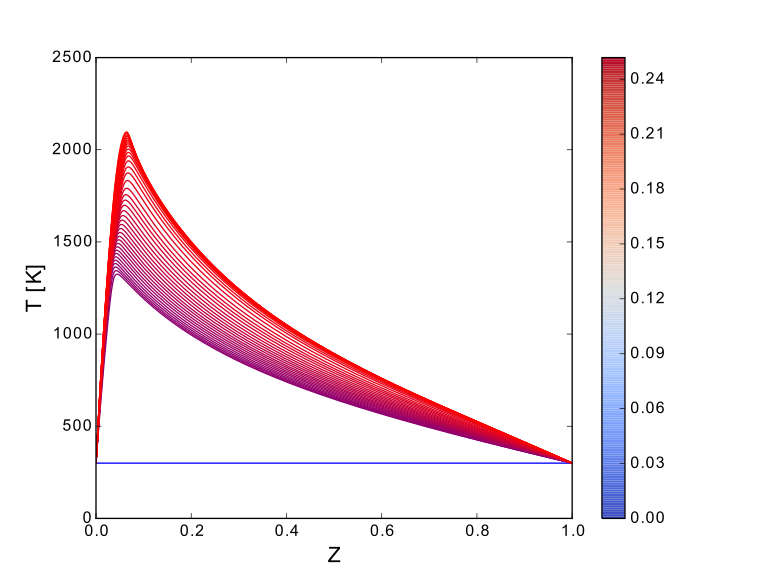
Diffusion flamelets colored by their value of the progress variable at the stoichiometric conditions(c_st).
Premixed Flamelet Capability
Premixed flamelets [2] are a different type of flamelet solution that can be computed using FlameMaster. These flamelets are solely used as part of the Pareto Efficient Combustion (PEC) framework in Loci-Stream. This framework allows for switching between diffusion flamelet table data, premixed flamelet table data, and detailed chemistry to allow for accurate and timely combustion simulations to be performed. The compressible table for premixed flamelets is activated using the FPIC` input file keyword to the Flamelet Table Tool. A new interpolation scheme was added to the Flamelet Table Tool because of the fundamentally different nature of the premixed flamelets compared to the diffusion flamelets, which can be seen by comparing the qualitative differences between the manifold shown below and the one for diffusion flamelets above.
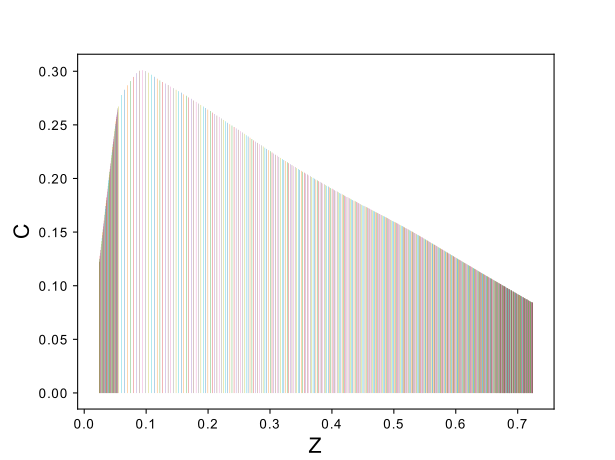
Premixed flamelets that make up the manifold for premixed flamelet tables.
A premixed flamelet table requires interpolation between each of the vertical individual premixed flamelets to obtain a value for the variable of interest at the Z, C location that is to be filled in the flamelet table as is shown below.
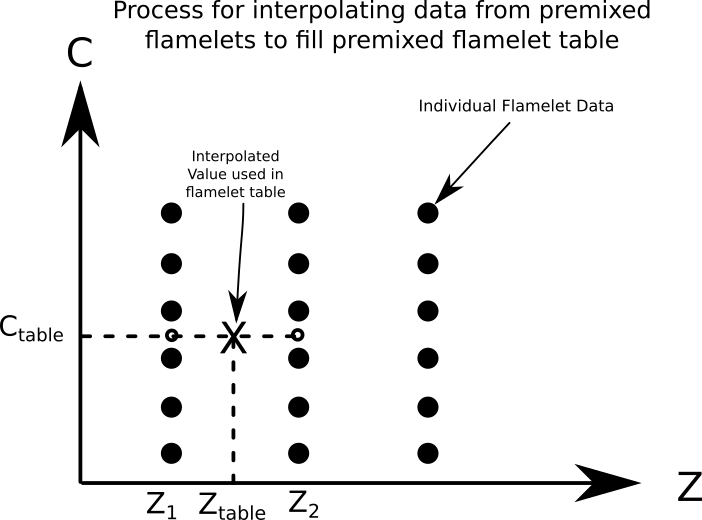
Premixed flamelet table interpolation process.
Data points that are outside of the flamelet manifold (the space of Z, C values where flamelet data exists) are extrapolated from the upper values of the flamelet solutions as shown below.
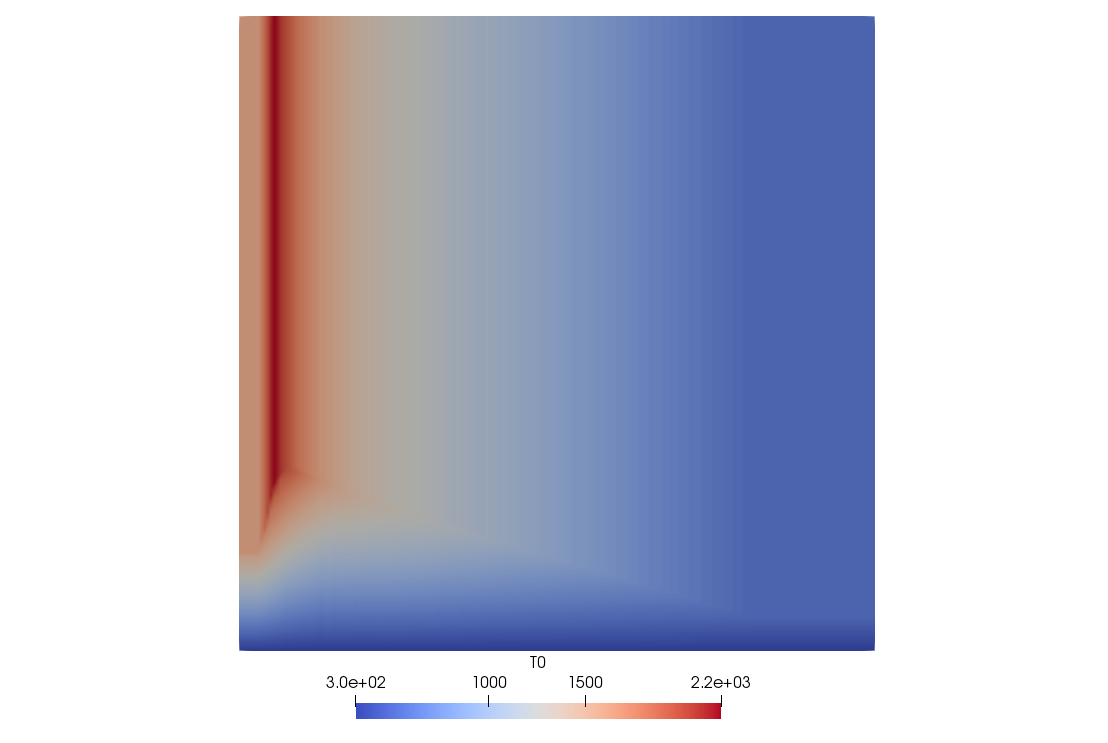
Temperature contours for a premixed flamelet table that was generated using the flamelet generation tool.